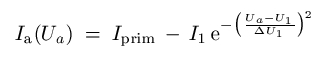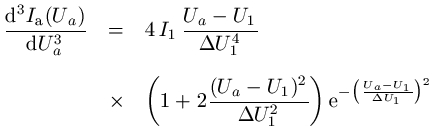Mein privater kleiner Teilchen-Beschleuniger

Ich habe immer meine Berufs­kollegen bewundert, die am LHC des CERN in Grenoble oder am Linear Accele­rator Center in Stanford auf die Suche nach den elementaren Bausteinen der Materie gehen durften: Quarks, W- und Z-Bosonen, das Higgs-Teilchen sind nur einige Beispiele, deren Nach­weis immerhin mit Nobel-Preisen gewürdigt wurde. Als einfacher Fest­körper-Physiker hat man diese Option nicht. Natürlich gibt es auch hier wahn­sinnig interes­sante Dinge zu finden. Da will ich mich nicht beklagen.

Doch so einen Teilchen-Beschleu­niger hätte ich auch ganz gern, wenn auch gewiss im Klein­format. Selbst­verständ­lich habe ich sofort an Elektronen­röhren gedacht. Nicht anders als an einem echten Beschleu­niger gibt es hier eine Vakuum­strecke, in die elektrisch geladene Teilchen - Elektronen - entlassen und dann beschleu­nigt werden, um schließ­lich mit einem anderen Objekt - der Anode - in Kolli­sion gebracht werden.

Allerdings fragte ich mich, was denn bei dieser Kollision Interes­santes passieren soll. Entstehen irgendwelche quanten­mecha­nischen Teilchen? Und wenn ja, wie weise ich diese nach? Und bei welcher Beschleu­niger-Energie, sprich Anoden­spannung, soll ich suchen? Ein W-Boson hat eine Energie von 100 Mega­elektro­nenvolt. Schön, aber 100 Milionen Volt Anoden­spannung schienen mir für den Anfang doch etwas zu ambitio­niert. Oder Röntgen­strahlen ? "Unter 10 Kilovolt kannst Du das vergessen", hat mir ein erfah­rener Kollege gesagt. Schwierig! Auf etwas Radio­aktives hatte ich ohnehin keine Lust.

Dann hatte ich die Lösung. Um es gleich zu sagen: besonders interes­sante Kollisions-Experi­ment mit Röhren und Elektronen gibt es bei besonders niedriger Anoden­spannung, bei unter 30 Volt. Das ist allemal einen Versuch wert.

Low Energy Electron Diffraction, kurz LEED, ist das Zauber­wort. Im den feinen Details des Anoden­strom der Röhre lassen sich die quanten­mecha­nischen Energien der Elektronen im Anoden­blech erkennen: Fermi-Energie, Austritts­arbeit sowie die soge­nannten Plas­monen, die Quanten der Ladungs­dichte-Wellen im Fermi-See, die für die Sekundär­emission sorgen. Dazu später mehr. Ein Oszi wird gebraucht und ein paar Strom­quellen. Der sonstige Schaltungs­aufwand ist denkbar gering.

Letzte Änderung: 18.4.2024

Zurück zur vorigen Seite

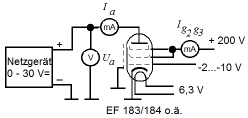
Mein erster Teilchenbeschleuniger

EF 184 und EF 183, zwei Pentoden aus dem TV-ZF-Verstär­ker, eignen sich vorzüg­lich für unseren Versuch. Dazu müssen sie als Tetrode geschal­tet werden.

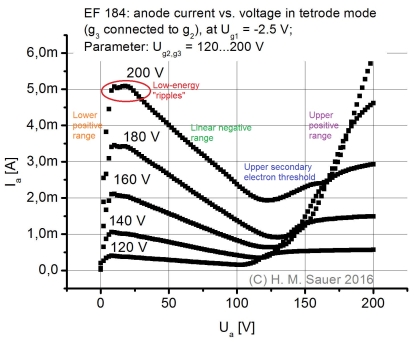
Unser Experiment funktio­niert wie die Messung einer Röhren­kenn­linie, und zwar derje­nigen des Negadyns, siehe Schalt­plan. Hierbei wird eine Pentode verwendet und als Tetrode geschaltet ist. Schirm- und Brems­gitter werden gemeinsam an eine hohe Span­nung gelegt. Diese beiden sehr stark positiv gela­denen Gitter sollen Sekundär­elektronen, die aus der weniger positiven Anode heraus­geschlagen werden, absaugen. Der Anoden­strom I_a wird nun als Funktion der Anoden­spannung U_a gemessen.
Trifft nun ein Elek­tron von der Kathode auf die Anode auf, dann können nämlich verschie­dene Dinge passieren:

1. Das Elektron wird vom Metall absorbiert, seine Energie wird in Wärme umge­wandelt. Das ist der Regel­fall. Die Anode wird einfach nur warm.

2. Ein inelastischer Stoß mit einem Elektron aus dem Anoden­metall. Dieses kann aus dem Metall heraus­gekickt werden. Es wird zum Sekundär­elektron. Der Anoden­strom reduziert sich, sobald die Anoden­spannung die nötige Schwelle übersteigt. Es ist wie beim foto­elektri­schen Effekt. Dort macht das halt ein Licht­quant, ein Photon. Ein direkter Stoß passiert zwischen Elek­tronen aber relativ selten.

3. Ein Plasmon entsteht. Das eintreffende Elek­tron erregt im Metall eine Ladung­sdichte­welle. Es ist wie wenn man einen Stein in einen stillen Teich wirft. Um die Eintauch­stelle breiten sich kreis­förmige Wellen auf der Wasser­ober­fläche aus. Ein Plasmon ist aber besonders: es hat im Gegen­satz zu einer gewöhn­lichen Welle eine bestimmte Mindest­energie. Diese hängt vom jewei­ligen Material ab. Wir sind nun mitten in der Quanten­mechanik. Bei Nickel, dem am meisten verbrei­teten Anoden­material, liegt die Plasmonen-Energie bei 12 eV. Doch das Plasmon behält seine Energie nicht, sondern zerfällt. Es gibt sie an eines der vielen Valenz­elektron des Metalls ab und tritt es wie einen Fußball hart aus dem Spiel­feld. Plasmonen entstehen recht oft beim Auf­schlagen eines Primär­elektrons passender Energie. Man kann die Energie­schwelle am Oszi als kleine Zacke sehen.

Plasmonen spielen im Alltag eine durchaus sichtbare Rolle. Das farbige Glas alter Kirchen­fenster enthält winzige minera­lische Farb­pigmente. Diese haben eine Plasmonen­energie von nur 2 bis 3 eV. Einfal­lendes Sonnen­licht mit dieser Frequenz wird davon absorbiert, und das Fenster erscheint in der entspre­chenden Komplementär­farbe. So haben schon die alten Meister rote, grüne, blaue und gelbe Gläser herge­stellt. Auch die moderne Nano­techno­logie weiß mit diesem Phänomen einiges anzufangen [8].

4. Manchmal wird ein Elektron vom atomaren Metall­gitter elastisch reflek­tiert wie ein Licht­quant an einem optischen Beugungs­gitter: Bragg-Beugung. Das wäre mit diesem Versuch aber nicht zu erkennen.

Die Suche nach den Events

Die Tetrodenkennlinie einer EF 184 besteht aus mehreren Teilabschnitten:
1.) Bei sehr niedriger Anoden­spannung < 10 V steigt der Anodenstrom an, um dann auf hohem Niveau zu sättigen.
2.) An der Sättigungs­kante bei 5 bis 30 V ist der Anoden­strom von einem wellen­förmigen Anteil überlagert. Das ist genau das Kenn­linien­gebiet, das uns interes­siert.
3.) Linear abfallender Kennlinien­bereich: der Anoden­strom nimmt gleich­mäßig ab, wenn die Anoden­spannung bis ca. 120 V weiter steigt. Die Anzahl der Sekundär­elek­tronen wächst propor­tional mit der Anoden­spannung. Das ist der ideale Arbeits­bereich eines Negadyns, zum Beispiel bei diesem Tongene­rator.
4.) Sättigung des Sekundär­stroms bei etwa 140 V. Der Anoden­strom hat ein Minimum, die Zahl der erzeugten Sekundär­elek­tronen ein Maximum.
5.) Im oberen positiven Kennlinien­abschnitt nimmt der Anoden­strom bei weiterer Erhöhung der Anoden­spannung bis auf das Niveau, das die Röhre in gewöhn­licher Pentoden­schaltung haben würde, rasch zu. Nicht alle erzeugten Sekundär­elektronen können den Einfluss­bereich der Anode mehr verlassen. Sobald U_a > U_g2 ist, funktio­niert unser LEED-Experi­mment daher nicht mehr.

Auf einer Ausschnitts­vergröße­rung der Kurve im Bereich von Anodens­pannungen von 0 bis 30 V kann man sich die "Wellig­keit" genauer ansehen. Ich habe hierzu den Anoden­strom der EF 184 mit einer erhöhten Auflö­sung der Anoden­spannung von 0,1 V bei einer Schirm- und Brems­gitter­spannung von 200 V gemessen.

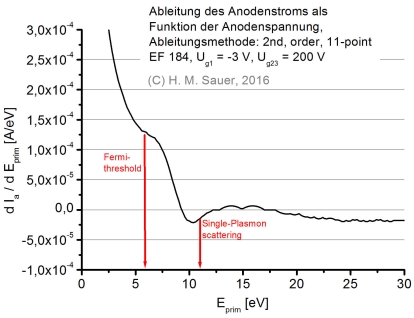
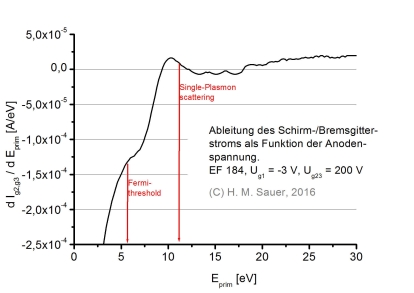
Hier der Schirm- und Brems­gitter­strom, bzw. seine Ableitung nach der Energie. Das Diagramm zeigt die gleichen Struk­turen invertiert, da an der Anode emit­tierten die Sekundär­elektronen alle genau hier, am positiv­sten Punkt der Röhre, ankommen.

Die Struktur erscheint klarer, wenn man die erste Ableitung des Anoden­stroms nach der Anoden­spannung ausdrucken läßt. Die Spannungs­achse gibt die Energie der Primär­elektronen in Elektronen­volt in eV an. Die an sich mehr oder weniger sanft gekrümmte Anoden­strom­kurve weist zwei markante "Zacken" auf, die wegen der Ableitung deutlich hervor­treten. In der dI_a/dU_a-Kurve entsprechen die Wende­punkte den Maxima dieser Zacken auf der Energie­achse:
1.) der Wendepunkt bei 5,5 eV ist die Austritts­arbeit des Anoden­blechs. Ein Primär­elektronen dieser Energie kann durch einen direkten Stoß ein einzelnes Elektron aus dem Metall heraus­schlagen.
2.) der Wende­punkt bei ca. 12 eV entspricht der Plasmonen­resonanz. Ab dieser Energie kannen das Elek­tron ein Plasmon erzeugen. Dieses erzeugt seiner­seits ein Sekundär­elektron.

Die übrigen kleinen Schwan­kungen erweisen sich als Störungen, die sich bei weiteren Mes­sungen nicht zuordnen lassen. Bei höheren Energien jenseits von 30 eV führt ein einfal­lendes Elektron mehrere Stöße aus. Die LEED-Struk­turen verschwim­men dann mitei­nander. Die Anzahl der erzeugten Plasmonen und daher der Sekundär­elektronen wächst propor­tional zur Energie des einfal­lenden Primär­elektons an. Das ist der lineare fallende Bereich der Tetroden­kenn­linie.

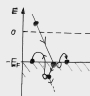
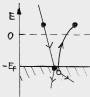
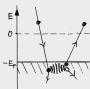
Energieschwellen = Wende­punkte der Mess­kurve

Wieso kann man an den Wende­punkten der dI_a/dU_a-Kurve die Energie­schwellen für Stoß­prozesse identi­fizieren ? Das ist ein alter Trick aus der Spektro­skopie: wenn die Energie E_a = e U_a des Elektrons genau einer solchen Schwelle bei E₁ = e U₁ entspricht, dann ist die Wahr­schein­lichkeit, dass es seine Energie überträgt, besonders groß. Infolge­dessen hat der Sekundär­strom einen wenn auch schwach ausge­prägten "Peak", d.h. ein, lokales Maximum, der Anoden­strom ein Minimum, etwa von der Form einer Gauß­schen Glocken­kurve:

Hierbei sind I_prim der Primär­strom, I₁ die Amplitude des Sekundär­strom-Maximums, des aus solchen Stößen resultiert, und ΔU₁ die Breite des Absorp­tions­maximums. Man sieht, an der Energie­schwelle nimmt der Anoden­strom gegenüber dem Normal­wert um den Betrag I₁ ab. Um zu zeigen, dass die dI_a/dU_a-Kurve exakt bei U_a = U₁ einen Wende­punkt hat, bilden wir einfach die dritte Ablei­tung d³I_a/dU_a³:

Der erste Term hat bei U_a = U₁ tatsäch­lich eine Null­stelle, und zwar die einzige in der Umgebung des Peaks. Womit die Sache bewiesen ist: die genaue Höhe der Energie­schwelle kann man am Wende­punkt der Strom-Spannungs­kurve ablesen (und nicht etwa in einem Maximum oder Minimum).

Weiterführende Literatur

[1] L. Austin, H. Starke, Ueber die Reflexion der Kathodenstrahlen und eine damit verbundene neue Erscheinung secundärer Emission, Ann. Physik 9, 27 (1902)

[2] E. M. Baroody, A Theory of Secondary Electron Emission from Metals, Phys. Rev. 78, 780-787 (1950)

[3] R. E. Simon, B. F. Williams, Secondary Electron Emission, RCA Electronic Components, David Sarnoff Research Center, 167-170 (1968)

[4] S. Andersson, Plasma Thresholds in the secondary electron yield - I. experiment, Solid State Commun. 11, 1401-4 (1972)

[5] S. Anderson, B. Kasemo, Low-Energy Electron diffraction intensities from the clean Nickel (100) Surface, Surface Science 25, 273-288 (1971)

[6] M. S: Chung, T. E. Everhart, Role of plasmon decay in secondary electron emission in the nearly-free-electron metals. Application to aluminum, Phys. Rev. B 15, 4699-4715 (1977)

[7] J. P. Ganachaud, M. Cailler, A Monte-Carlo Calculation of the secondary electron emission of normal metals, Surface Science 83, 498-518 (1979)

[8] V. Temnov, U. Woggon, Nanoplasmonik in Hybridstrukturen, Physik-Journal 9 (6), 45-50 (2010)

Klappt es auch mit anderen Röhren?

1.) Der LEED-Versuch klappt mit nahezu allen gängigen Pentoden. Voraussetzung ist, dass das Bremsgitter nicht intern mit der Kathode verbunden ist: EF 80, 86, 89, EL 80, EL 34, 6L6GC wären weitere Typen, die mir spontan einfallen. EL 84, EL 95, PL xx und 6V6GT scheiden wegen ihres fest verdrahteten Bremsgitters dagegen aus.

2.) Ich hatte zur Aufnahme der Kennlinien zwei Source Meter Units vom Typ Keithley 2400 und Labview zur Verfügung sowie ein paar tüchtige E-Technik-Stu­denten der TU Darmstadt. Hat nicht jeder. Die Daten­auswer­tung habe ich mit Origin(R) gemacht. Dieser für den Bastler unübliche Aufwand macht die Arbeit zwar äußerst bequem und präzise, aber fürs Prinzi­pielle ist das purer Overkill. Mit Oszi, einem Trafo mit 20 bis 40 V Ausgangs­spannung für die Anode sowie einer Strom­quelle für die 200 V Schirm­gitter­spannung sieht man alles ganz genau so gut wie hier. Ein digi­tales Oszi ist natürlich praktisch, damit man die Mess­daten zum Beispiel in MS-Excel laden und dort analy­sieren kann.

3.) Ich habe ein wenig Literatur aus wissen­schaftlichen Zeit­schriften gesammelt. Ich habe das vor allem deshalb getan, um einen Vergleich zwischen den hier gezeigten Kurven und den dort bespro­chenen LEED-Spektren zu ermög­lichen. Daher habe ich eine Bitte: beim Auf­schlagen nicht erschrecken! Im Detail steckt hinter Elektron und Plasmon wie auch hinter der Technik der Elektronen­röhren selbst hammer­harte Quanten­mechanik

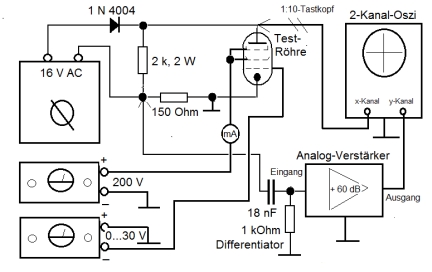
Die Schaltungsvariante mit Oszil­loskop und ohne aufwän­digen Kenn­linien­schreiber

Eine dicke Leistungspentode...

Eine EL 34 wollte ich auch mal unter die Lupe nehmen. Das Verhalten ist im Detail, aber nicht grund­sätzlich von dem der EF 184 verschieden. Kein Wunder: die Anode besteht ebenfalls aus Nickel­blech.
Das LEED-Expe­riment gelingt auch direkt am Oszi. Ein Zwei­kanal­gerät ist dabei zweck­mäßig. An einem Kenn­linien­meßstand mit hoch­wertigen Source-Metern hat man bei der Strom­messung ohne weiteres 7 oder 8 Dezimal­stellen Auflö­sung - darum sind diese Mess­geräte so extrem teuer. Man kann sich wunderbar in die Details der Anoden­strom­kennlinie hinein­zoomen und Fein­heiten studieren. Mit einem gewöhn­lichen Digital­oszi geht das nicht so einfach. Meines beispiels­weise digita­lisiert die Messwerte mit einem 8-Bit-AD-Wandler. Die Auflösung ist daher auf 1/256 des Meß­bereichs begrenzt: 0,4 %. Das ent­spricht ungefähr 2 1/2 Dezimal­stellen. Sogar damit läßt sich der Versuch machen, doch man sieht nur wenig Details. Wir nehmen daher einen analogen Mess­verstärker zur Hilfe, um den interes­sierenden Anteil des Mess­signals auf den Arbeits­bereich des AD-Wandlers heraus­zufiltern und zu verstärken. Natürlich ist auch unser Mess­ver­stärker selbst­gebaut.

Der neue Messaufbau

Der Versuchsaufbau: Den Anoden­strom erzeugen wir nun mit einem 16-Volt-Trafo von der Spiel­zeug­eisen­bahn. Mit der Diode entfernen wir zunächst die negative Halbwelle. Den Anoden­strom messen wir dann über den Spannungs­abfall am einge­zeichneten 150-Ohm-Widerstand. Die Meß­spannung wird mit der Kombi­nation aus 18-nF-Konden­sator und 1-K-Wider­stand auf analogem Wege zeitlich diffe­renziert. Der Meßver­stärker setzt das Niveau des Signals dann auf einige Volt herauf. Erst jetzt wird das Signal vom Oszi (falls es nicht ein analoges mit Kathoden­strahlen ist) digita­lisiert. Das ist mess­technisch sehr viel günstiger. Die übrigen Strom­quellen sind für Schirm­gitter (200 V) und Steuer­gitter (0...-30 V). Über die Steuer­gitter­spannung wird der Schirm­gitter­strom auf wenige mA einge­stellt. Wichtig: alle Masse­anschlüsse solten an einem Punkt zusammen­laufen, nämlich an der Eingangs­masse des Meßver­stärkers. Das redu­ziert die Stör­spannungen erheblich.

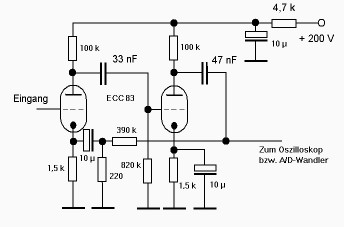
Ein kleiner Verstärker verbessert die Auflösung

Als Mess­verstärker verwende ich einen sehr bewähr­ten, zwei­stufigen Trioden­verstärker mit einer ECC 83. Die Verstär­kung ist ziemlich genau auf 1000:1 eingestellt, also auf 60 dB. Dies wird mittels Gegen­kopplung des Ausgangs­signals auf die Kathode der ersten Triode erreicht. Dazu dient die Kombi­nation aus den Wider­ständen mit 390 kΩ und 220 Ω, die einen Spannungs­teiler bilden. Das Gitter der ersten Triode wird mit dem 1-kΩ-Wider­stand im Diffe­renzier­glied der Mess­schaltung verbun­den. Zwischen 20 Hz und 40 kHz ist die Verstär­kung relativ konstant. Die Betriebs­spannung wird aus dem 200-Volt-Netz­teil bezogen, das auch Schirm- und Brems­gitter der getesteten Pentode versorgt.

Der Schaltplan

Das differenzierte Messsignal

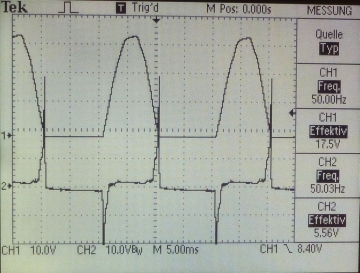
Schon das erste Oszil­logramm zeigt den Effekt:

Kanal 1 (oben) zeigt die positiven Hälften der 50-Hz-Sinus-Spannung, die der Eisen­bahn­trafo an die Anode liefert. Es hat 35 V in der Spitze.

Kanal 2 (unten) zeigt das differenzierte und verstärkte Signal des Anoden­stroms, das am Ausgang des Verstär­kers erscheint. Die hohen Spannungs­spitzen am Anfang und Ende der Halb­welle igno­rieren wir und zoomen uns mit dem Oszil­loskop in die feinen Details, die dazwi­schen nahe der Null­linie zu sehen sind.

Auswertung: Wir verglei­chen diese feinen Struk­turen mit den jeweiligen Anoden­span­nungen. Es empfiehlt sich, am Oszil­loskop mit der "Aquire"-Option über eine gewisse Anzahl von Peri­oden des Signals zu mitteln. Dadurch lassen sich Rauschen und Stö­rungen stark reduzieren. Das Nutz­signal, die Spuren des Elektronen­aufpralls auf dem Anoden­blech, die mit den Ener­gie­schwel­len zusam­men­hängen, tre­ten jedoch hervor.

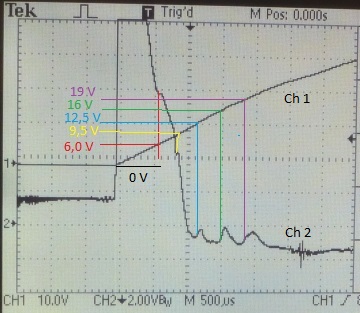
Plasmonen am Fuß der Messkurve

An der ansteigenden Flanke der Halbwelle aufge­nommen: Ich habe die Impulse des Sekundär­stroms aus Kanal 2 mit farbigen Linien markiert und mit den Anoden­span­nungen aus Kanal 1 verbunden, die den verschie­denen Streu­effek­ten mit Plas­monen und anderem ent­spre­chen könn­ten. Die Wende­punkte der Mess­kurve erschei­nen genau dann, wenn die Anoden­span­nung bei 6, 9.5, 12.5, 16 und 19 Volt liegt. Dis auf einen kleinen Versatz und den Wende­punkt bei 9.5 V stimmt das gut mit der Kurve rechts im Bild überein.

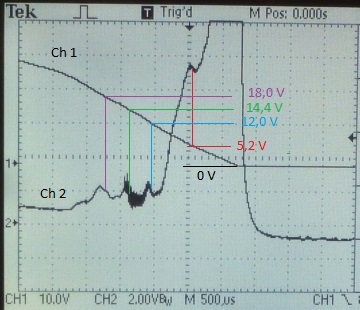
...und hier wieder in der abfallende Flanke der Kurve

An der abfallenden Flanke ergibt sich logischer­weise ein spiegel­bild­liches Signal. Die Wende­punkte liegen bei etwa 5.2, 12.0, 14.4, 18 Volt. Bei den ersten beiden handelt es sich wieder um die Austritts­arbeit und die Plasmonen­resonanz. Die beiden höheren Werte entsprechen vermutlich Sekundär­elektronen, die Energie von gleich zwei oder mehr Plas­monen erhalten haben. Es könnte natür­lich auch sein, dass es noch andere Über­gänge mit Elek­tronen gibt. Diese Mes­sung beweist ferner, dass die Wellig­keit des Mess­signals keine simple Nach­schwingung im Signal­ver­lauf ist, sondern tatsäch­lich eine Abhäng­igkeit der momen­tanen Anoden­span­nung zeigt.